YACHTSEGELSCHULE KARLSRUHE SPORTBOOTFÜHRERSCHEINE THEORIEKURSE PRAXISAUSBILDUNG
Segelphysik Radar Astro-Nav ...
Animationen für Yachtsegler
"Eine Animation beschreibt mehr als 1000 Fallbeispiele!"
Animation zum Selbststudium
Vorwort des Autors
Segel-Animationen...
Was heißt das? Nun, was Animationen sind weiß wohl jeder. Über die Jahre, in denen ich Kurse gegeben habe, kam immer mal wieder Lernstoff auf, der entweder nur anhand statischer Zustände, also bestimmter Fälle, zu beschreiben war, oder aber zu seiner Erklärung hätte es viele, teilweise sehr viel mehr Worte gebraucht, um die beteiligten Komponenten und ihre wechselseitigen Zusammenhänge einigermaßen zu beschreiben. Da viele - so wie ich auch - am besten mit Bildern lernen können, stellte ich mir die Aufgabe, die fraglichen Zusammenhänge in Form von bedienbaren Animationen (-> variablen Grafiken) darzustellen. Damit kann ein Parameter in seinem üblichen Bereich meist fließend verändert werden, und die Animation zeigt dann grafisch das Resultat durch die Änderung der Einflussgröße(n).
Wir schreiben heute 2021. Da zwischenzeitlich der Adobe Flash-Player aus Gründen der Sicherheit von Adobe abgekündigt wurde, der Flash-Player nicht mehr erhältlich ist und zudem die Browser-Hersteller seit Anfang dieses Jahres das Abspielen von Flash-Inhalten verhindern, bleibt mir nichts anderes übrig, als die Animationen nach und nach in andere Sprachen zu übertragen. Ja, das dauert seine Zeit, aber wir sind auf einem guten Weg und einige der wichtigeren sind bereits umgesetzt. Dabei kommt dem Anwender zudem zugute, dass die Animationen durch Verwendung anderer Frameworks auch auf Mobil-Geräten bedienbar werden. (Umgesetzt ist eine Animation hier, wenn der Link zu einer JavaScript bzw. JavaScript/ZIM Animation führt.)
Sollte die gewählte Animation noch nicht umgesetzt sein, bitte ich noch um etwas Geduld und empfehle, in Bälde noch mal vorbeizuschauen oder mich zu kontaktieren.
Und nun viel Spaß und tiefgreifende Erkenntnis mit dem Stoff!
Daniel P.
Animationen zum Selbststudium
Animation - Radar/Seerecht
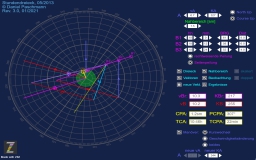
Radarplotting
Radar-Plotting ist eines der systematischen Mittel zur Bestimmung, ob sich die Möglichkeit der Gefahr einer Kollision entwickelt, die in den Kollisionsverhütungsregeln angesprochen werden.
Jeder Radarbeobachter - und damit auch jeder Sportschiffer, der sich entweder der SSS-oder der SHS-Prüfung stellt, muss dieses Verfahren kennen und können.
Für die wesentlichen Eigenschaften stehen Eingabefelder zur Verfügung: eigener Kurs und Geschwindigkeit, der Radius des Nahbereiches, Eingabefelder für bis zu drei Beobachtungen eines Gegners, und ob die Peilungen rechtweisende oder Seitenpeilungen sind.
Die Berechnungen erfolgen auf nur zwei Beobachtungen, wenn die dritte Beobachtung nicht später als die zweite eingegeben wurde.
Hier wird das Stundendreieck immer an die vorletzte Beobachtung gezeichnet, denn ab dem Zeitpunkt ist der letzte Kurs stabil.
Damit ist auch gleichzeitig mehr Platz frei für das Zeichnen des Dreiecks für das Ausweich-Manöver.
Diverse Check-Boxen erlauben das Ein- bzw. Ausblenden verschiedener Zeichnungsdetails. Auch kann die Zeichnung vergrößert (2:1) oder verkleinert (1:2) werden, wenn der Maßstab ungeeignet ist.
Wie im richtigen Leben auch kann das Ausweich-Manöver alleine durch Kursänderung, durch die Änderung der Geschwindigkeit aber auch durch beides erfolgen.
Zunächst werden durch Aktivieren von "Manöver" eigener Kurs und Geschwindigkeit übernommen. Entsprechend der Wahl können nun selektiv Parameter eingestellt werden.
Zur Beachtung: Selbst wenn das Ausweich-Manöver (zeichnerisch) zu einem sicheren Nahbereich führt, ist das Manöver auf alle durch die KVR formulierten Nebenbedingungen hin zu überprüfen (Kursänderung groß genug, kein Queren vor dem Bug des Gegners u.v.a.m.).
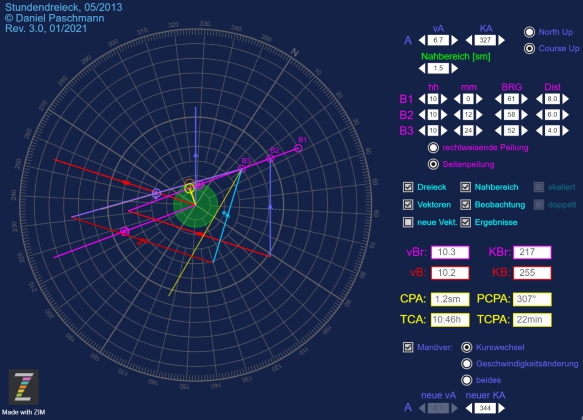
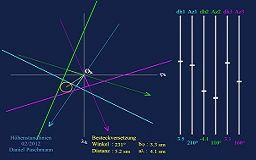
Mit systematischen Mitteln feststellen ob Kollisionsgefahr besteht
Durch Einzeichnen der letzten Beobachtungen eines potentiellen Kollisionsgegners können dessen wahrer Kurs und dessen Geschwindigkeit ermittelt werden. Mit dieser Kenntnis lässt sich anschließend - im Falle einer bestehenden Kollisionsgefahr - ein geeignetes Ausweichmanöver bestimmen.
Animation – Radar
Azimutale Auflösung
Diese Animation soll verdeutlichen, unter welchen Umständen zwei gleichweit entfernte Radar-Objekte in unterschiedlicher – jedoch fast gleicher Richtung als einzelne Ziele erkannt werden.
Die Frage danach hat sehr reale Hintergründe: In welcher Entfernung kann ein Radargerät die nahe gelegenen Begrenzungen einer Hafeneinfahrt überhaupt sehen?!
Die Antwort erscheint trivial: Um zwei Objekte in gleicher Entfernung – jedoch unterschiedlicher Peilung als einzelne zu erkennen, muss der Radarstrahl deutlich zwischen die beiden Objekte passen. Tut er das nicht, dann trifft der Strahl ja noch auf das eine und schon auf das andere.
Hier gehen die drei Komponenten des Problems ein:
- Die Breite der Radarkeule. Sie ist größer bei Strahlern mit weniger Schlitzen.
- Der azimutale Abstand beider Objekte … , der verständlicherweise größer sein muss als die Breite der Strahlkeule.
- Die Ausdehnung der Objekte. Naja, das könnte man auch mit dem vorhergehenden Punkt zusammenfassen.
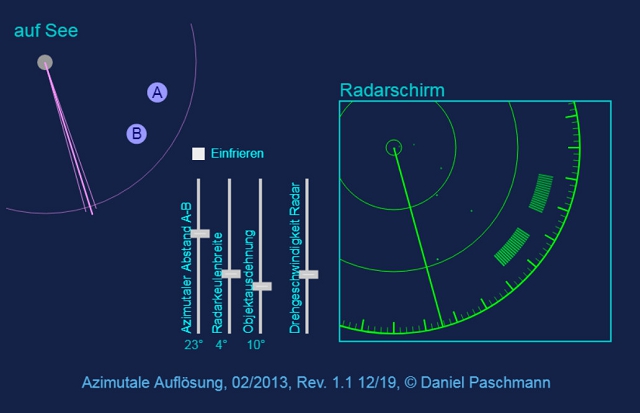
Auflösung einzelner Objekte mit unterschiedlichem Azimut
Unter welchen Umständen werden zwei gleichweit entfernte Objekte, die in verschiedenen Peilungen geortet werden, als einzelne getrennte Objekte erkannt.
Animation – Radar
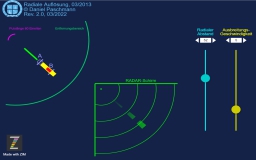
Radiale Auflösung
Bei der Radialen Auflösung geht es im Unterschied zur Azimutalen Auflösung um das die Distanz: Zwei Objekte befinden sich in gleicher Peilung zur Radarantenne, jedoch ihr Abstand zur Antenne ist leicht unterschiedlich. Wann werden sie auf dem Radarschirm als einzelne Objekte angezeigt?
Hier spielt die Dauer des Radarpulses die entscheidende Rolle.
Solange das Radargerät aktiv aussendet, bewegen sich die elektrischen Wellen von der Antenne weg – mit Lichtgeschwindigkeit. D.h., dass die Aussendung - "das Paket" - durch ihre Dauer einer Entfernung bzw. einer entfernungsmäßigen Länge entspricht.
Wenn die Entfernung, die das zum entfernteren Objekt ausgesendete „Paket“ zurücklegen muss, größer ist als die Länge des Pakets, dann trifft offenbar das vom entfernteren Objekt zurückgeworfene Paket später ein als das Ende des Pakets vom näheren Objekt.
Und das ist genau dann der Fall, wenn die Entfernung zwischen beiden Objekten mindestens halb so groß ist wie die Länge des Pakets, denn das Paket braucht vom näheren zum entfernteren die halbe Zeit und die andere Hälfte der Zeit für den Weg zurück zum näheren.
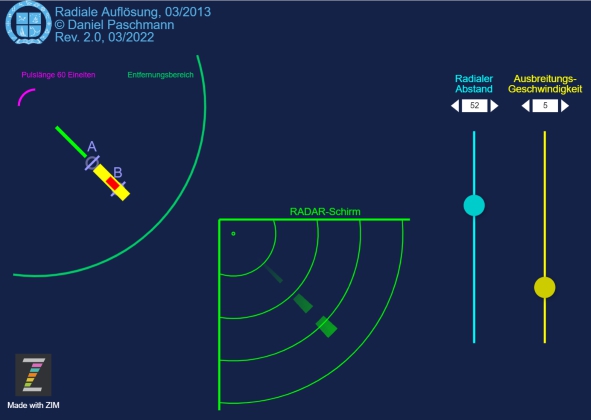
Auflösung einzelner Objekte in unterschiedlicher Entfernung
Unter welchen Umständen werden zwei unterschiedlich weit entfernte Objekte in gleicher Peilungen als einzelne getrennte Objekte erkannt.
Animation - Radar
Schlitzstrahler
Zeigt das Funktionsprinzip der Schlitzstrahlerantenne unserer Yachtie-Radargeräte - und natürlich auch größerer – durch die Überlagerung von Wellenfronten im zentralen Bereich der Antenne.
Jeder der Schlitze erzeugt für die Zeit der Aussendung des Radarpulses die Wellenberge und Wellentäler. Diese sind umso mehr gebündelt – ihre Wellenfronten überlagern sich also recht akkurat – je näher sie entlang der Senkrechten zur Antenne, also zur Hauptrichtung verlaufen.
Seitlich davon überlagern sich die Wellen stark ungeordnet, weshalb eine Bündelung nicht stattfindet, stattdessen sich die Aussendung "kreuz und quer" zusammensetzt genauso wie dann die reflektierten Wellen. Deshalb wird zumeist außerhalb der zentralen Richtung kein Ziel erkannt.
Die Animation zeigt auch, dass die Bündelung immer besser wird, je mehr Schlitze in der Antenne verbaut sind.
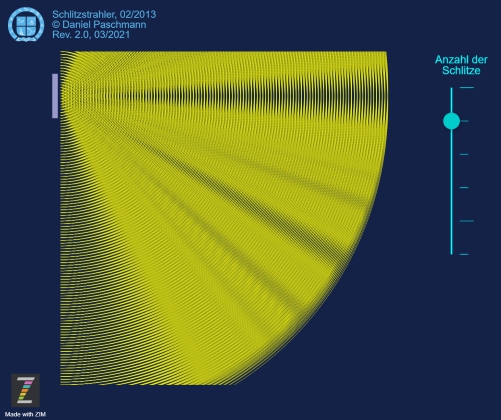
Funktionsprinzip eines Schlitzstrahlers
Präzise Überlagerung von seitlich versetzt ausgesendeten elektrischen Wellen.
Animation - Segelphysik
Luvgierigkeit
Jedes Segelboot kann durch bestimmte Maßnahmen mehr oder weniger luvgierig getrimmt werden. Dabei ist das grundsätzliche Vorhandensein einer gewissen Luvgierigkeit schon erwünscht. Andererseits kann bei schlechterem Trimm auch der Druck auf das Ruder so hoch werden, dass der Rudergänger sich ständig ins Zeug legen muss, um das Schiff auf dem Kurs zu halten, mal ganz davon abgesehen, dass die Yacht unter der Bedingung auch nicht mehr mit größtmöglicher Geschwindigkeit unterwegs ist. Übertreibt man, dann ist das Schiff vielleicht bereits leegierig. Hat man zuviel Tuch gesetzt, kann die Luvgierigkeit gar nicht mehr ausgeglichen werden, ist das Verhältnis zwischen Vor- und Hauptsegel ungünstig, wird eine künstliche Luv- oder Leegierigkeit erzeugt.
Bitte beachten: Der grüne Pfeil am Bug bildet keine absolute Größe der Luvgierigkeit ab, jedoch zeigt er deutlich die Tendenz einer Maßnahme. Er zeigt nach mehr oder weniger links für größer werdende Luvgierigkeit, zeigt er nach rechts, dann ist das Schiff leegierig getrimmt.
Die Steuerung des Trimmes erfolgt über die Größe des Großsegel und die der Genua, dem Vorsegel, sowie etwas durch das Stauen. Sind alle Getränke weit vorne im Bug gestaut, kann man damit die Luvgierigkeit erhöhen.
Größten Einfluss auf die Luvgierigkeit hat die Krängung durch den Wind. Deshalb besser eingerefft fahren, um nicht den „Sonnenschuss“ zu riskieren.
“Abdunkeln“ zeichnet die Konturen unseres Bootes dunkler, mit „Begrenzen“ wird die Krängung auf 40° beschränkt, „Leegierig“ und „Luvgierig“ zeigen das entsprechende Kräftepaar und die Wirkungspfeile, und „Segelpunkte“ zeigen die Unterdruckpunkte beider Segel entsprechend des gesetzten Tuchs.
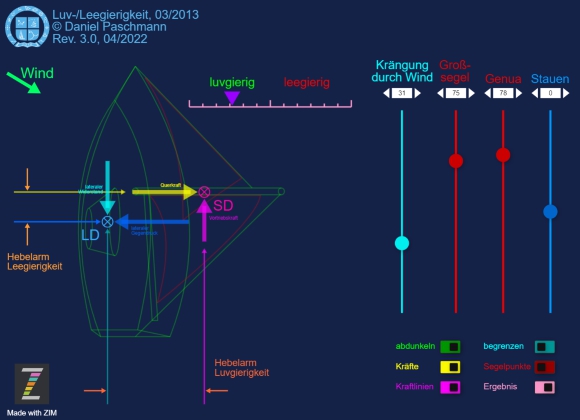
Segeltrimm auf dem Trockenen
In dieser Animation lässt sich leicht die Wirkung eine Maßnahme für oder gegen die Luvgierigkeit (Leegierigkeit) erfahren.
Animation - Segelphysik
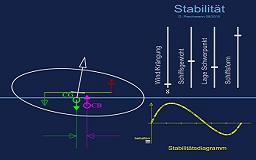
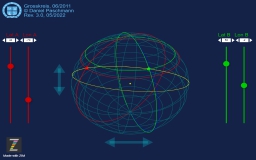
Stabilität
Stabilität ist eines der wichtigsten Kriterien beim Design eines jeden Schiffes und natürlich überlebenswichtig im täglichen Betrieb, wenn das Schiff z.B. durch schwere See oder bei starkem Wind unterwegs ist.
Dann nämlich wird das Schiff krängen, sich über eine Seite neigen. Die Eigenschaft, der Krängung eine aufrichtende Kraft bzw. ein Kraftmoment entgegenzusetzen, wird Stabilität bezeichnet.
Die aufrichtende Kraft soll umso größer sein, je weiter sich das Schiff zur Seite lehnt. Das geht – wie zu sehen sein wird – in den meisten Fällen nur bis zu einem gewissen Punkt – dem Punkt der verschwindenden Stabilität. Die Begriffe Formstabilität bzw. Gewichtsstabilität spielen hier die entscheidende Rolle.
Das Prinzip unseres Animationsschiffes ist dem gleich draußen in der Wirklichkeit.
Mit dem Regler „Schiffsform“ lässt sich eine Form wählen, die eher „formstabil“ ist, nämlich mit einem breit auf dem Wasser liegenden Schnitt. Das Gegenteil ist ein „gewichtsstabiles“ Schiff, eher schlank und mit einem großen Kielgewicht ausgerüstet. Gängige Yachten vereinen um die 30% ihres Gesamtgewichtes im Kiel.
Wie schwer die Yacht ist und wo circa der Masseschwerpunkt (CG = Center of Gravity) der Yacht zu liegen kommt, kann mit den beiden anderen Reglern gewählt werden.
Durch stufenlose Krängung von 0° bis 180° wandert nun der Auftriebsschwerpunkt (CB = Center of Buoyancy) aus und die Animation berechnet für den jeweils aktuellen Wert das resultierende Kraftmoment und zeichnet die Punkte in das Diagramm, sodass sich am Ende eine Stabilitätskurve ergibt.
Ist "behalten " ausgewählt, kann ein Parameter verändert werden, um dann die Kurve neu zu zeichnen. Auf diese Weise lassen sich Auswirkungen durch Parameterveränderung leicht miteinander vergleichen.
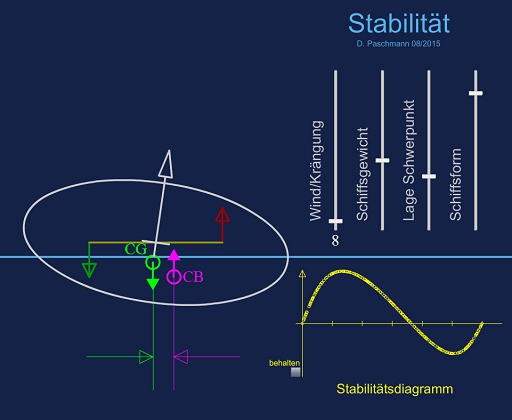
Real berechnete Stabilitätskurve
Das Animationsschiff ist zwar keine schnittige Hochseeyacht sondern eher eine Lenor-Flasche, die auf dem Wasser dümpelt, jedoch das Prinzip der Stabilität für beide Schwimmkörper gleich.
Animation - Segelphysik/Bootsbau - Javascript
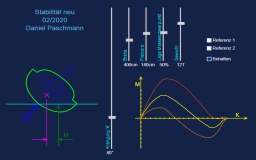
Stabilität 2
Beschreibung kommt in Kürze ...
Vorab:
Aktiviere "Referenz 1" oder "Referenz 2" und fahre die Kurve einmal durch. Danach "Behalten" anklicken und Referenz deselektieren, um die Kurve als Referenz zu speichern.
Die gelbe Kurve wird bei jeder Parameter-Änderung neu gezeichnet.
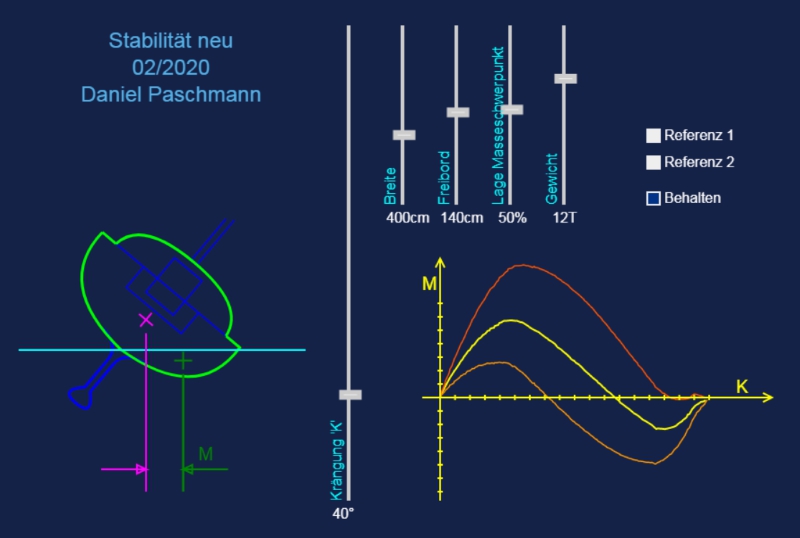
Ein Cruiser auf dem Prüfstand
Wie stabil ist eine Yacht bei Krängung? Probieren Sie es aus indem Sie verschiedene Parameter verändern.
Animation - Segelphysik
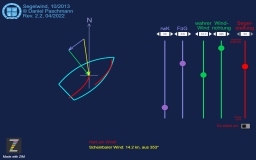
Scheinbarer Wind
Für ein Segelschiff ist der entscheidende Wind der sogenannte scheinbare Wind. Solange das Schiff noch keine Fahrt macht, ist der scheinbare identisch mit dem wahren Wind.
Der Wind steht in die Segel, und wenn alles richtig ist, dann nimmt das Schiff Fahrt auf – es kommt ein weiterer Wind hinzu, nämlich der Fahrtwind.
Diese drei Windkomponenten bilden ein Kräftedreieck; zwei davon sind real existierend – die dritte, der scheinbare Wind, eine abgeleitete bzw. rechnerische Größe, die gleichwohl diejenige ist, die unser Schiff antreibt und nach der wir uns zum Schluss richten müssen.
Hier ist alles wählbar: die Richtung, aus der der wahre Wind kommt, und dessen Stärke sowie die Kielrichtung des Segelschiffes und seine Geschwindigkeit, ausgedrückt in der Geschwindigkeit des Fahrtwindes.
Aus diesen Kraft- und Richtungskomponenten berechnet diese Animation den scheinbaren Wind in der Form seiner Richtung und seiner Geschwindigkeit.
Für die Segelstellung ist der scheinbare Wind entscheidend, woraus die empfohlene Großsegelstellung bzw. der ausgerufene Kurs zum Wind berechnet wird.
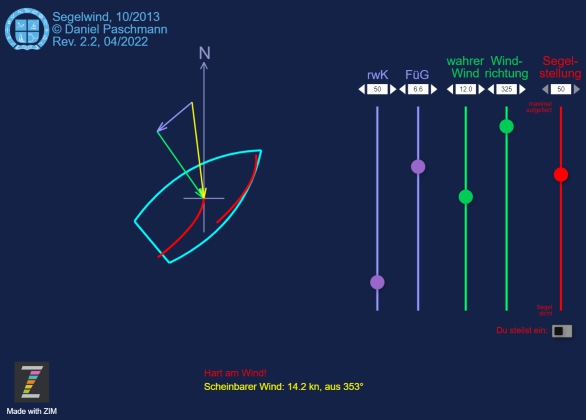
Die Zusammensetzung des scheinbaren Windes
Zwar nur eine abgeleitete Größe aus dem wahren Wind und dem Fahrtwind, aber gleichwohl diejenige, die unser Schiff antreibt und nach der wir unsere Segel einstellen müssen.
Animation - Komponenten
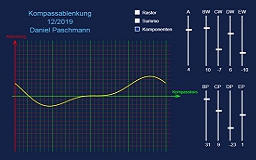
Ablenkungen Magnetkompass
Die Fehlerkomponenten, die eine Auswirkung auf die Ablenkung unseres Magnetkompasses haben, und wegen derer der Schiffskompass zu kompensieren ist, sind letztendlich 5 an der Zahl.
Alle fünf zusammengenommen ergeben eine individuelle Ablenkungskurve, die sich üblicherweise in der Ablenkungstabelle wiederspiegelt.
Andererseits kann die Ablenkungskurve definitiv nicht jede beliebige Form annehmen, weil es eben nur diese fünf in der Mehrzahl sinusförmigen Komponenten gibt, aus denen sich die Kurve zusammensetzt.
Die erste ist vorhanden, wenn der Kompass relativ zur Kielrichtung verdreht eingebaut wurde (A).
Magnetismus durch verbaute Einrichtungen (magnetisches Metall, elektrische Leitungen und Geräte) einmal entlang der Kielrichtung und einmal seitwärts davon sind zwei weitere (B und C). Beide haben ihre eigene Größe (W), die sich in einem jeweiligen Ablenkungswinkel ausdrückt, und eine Richtung (P), in der die Größe maximal ist.
Die beiden letzten Anteile kommen durch Weicheisen, also nicht magnetischem Metall, wie beispielsweise dem Motorblock aus gegossenem Aluminium oder Gusseisen. Wenn Kompass, einer der magnetischen Pole und eine solche Einrichtung sich in einer Linie befinden, werden die magnetischen Feldlinien im Weicheisen konzentriert, stärker als z.B. in der umgebenden Luft, weshalb sich eine Art flüchtiger Magnet in dieser Richtung ausbildet. (Man kennt das, wenn man z.B. eine spezielle Getränkebüchse neben den Kompass bringt.) Das zweimal (D und E) für eine ganze Schiffsdrehung. Auch hier wieder Stärke (W) und Maximalrichtung (P).
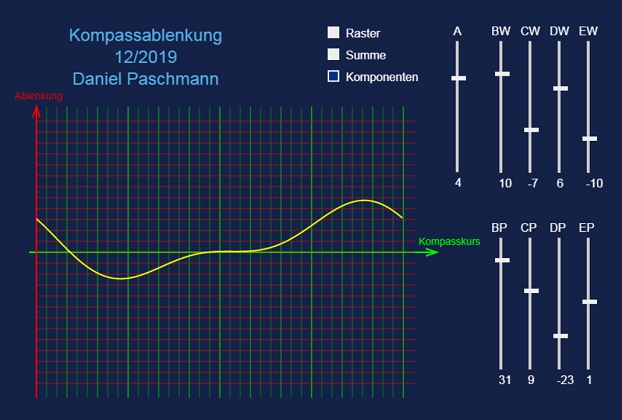
Die zusammengesetzte Magnetkompassablenkung
Die richtungsabhängige Ablenkung des Magnetkompasses setzt sich aus 5 zum Teil komplexen Anteilen zusammen.
Animation - Funk
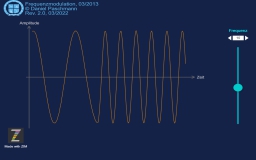
Amplituden-Modulation
Die Amplitudenmodulation war wohl historisch die erste Modulationsart, mit der komplexere Signale (z.B. Sprache) übertragen werden konnten. Und sie ist heute nach wie vor weltweit in Nutzung.
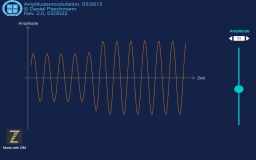
Die Amplitude einer meist sinusförmigen Grundschwingung wird in ihrer Größe zwischen klein und groß durch ein Steuersignal verändert und ausgesendet.
Wenn der Empfänger die Amplitude des aufgenommenen Signals fließend bestimmen kann – und das passiert im Demodulator -, dann kann das Orginalsignal wieder recht präzise hergestellt werden.
Diese Darstellung zeigt nur die sinusförmige Grundschwingung, das Steuersignal und das resultierende amplitudenmodulierte Signal. Sie dient nur der Veranschaulichung des Prinzips.
Zur JavaScript/ZIM Animation ...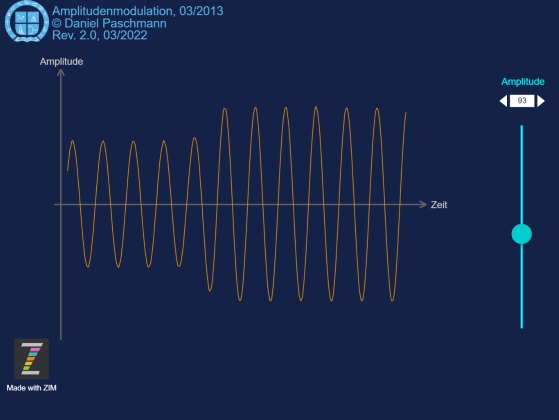
Modulation der Signalamplitude
Mit Hilfe eines Steuersignals wird die Amplitude einer Sinusschwingung über die Zeit verändert und das resultierende Signal zum Beispiel über eine Antenne ausgestrahlt.
Animation - Funk
Frequenz-Modulation
Auch mit der Frequenzmodulation sollen komplexe Daten übertragen werden, in dem ein Sender die Frequenz einer Sinusschwingung permanent in einem bestimmten Bereich entsprechend der zu übertragenden Information variiert.
Mit diesem Verfahren ist die Übertragung insgesamt sicherer als bei der Amplitudenmodulation, da die Information nicht in der Signalamplitude steckt, die z.B. durch atmosphärische Störungen beeinflusst – also verfälscht werden kann.
Auch diese Darstellung dient nur der Veranschaulichung des Prinzips.
Die Grundschwingungsfrequenz wird in Abhängigkeit des Steuersignals (hier) verkleinert. Verschiedenen Varianten werden eingesetzt, wie die erzeugte Frequenz gesteuert wird.
Digitale Übertragungen verwenden für die Übertragung der beiden binären Zustände zwei definierte Frequenzen, die sich z.B. um 1.200 Hz voneinander unterscheiden bei einer Grundfrequenz von beispielsweise 158,56 MHz. Eines dieser Verfahren wird im Zusammenhang mir der Übertragung de DSC-Informationen im UKW-Bereich verwendet oder bei der Übertragung von Wetterfax-Karten über Kurzwelle und nennt sich dort FSK (Frequency Shift Keying) .
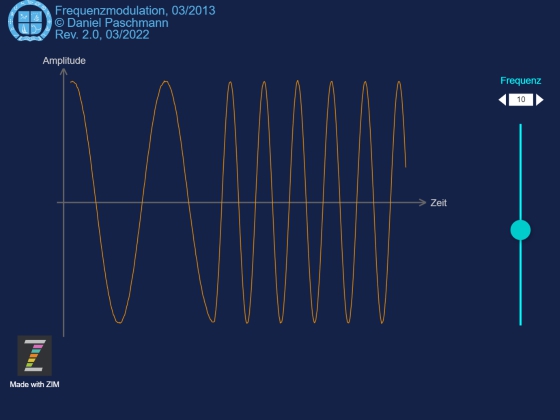
Modulation der Signalfrequenz
Mit Hilfe eines Steuersignals wird die Frequenz einer Sinusschwingung über die Zeit verändert und das resultierende Signal zum Beispiel über eine Antenne ausgestrahlt.
Animation - Astronavigation
Meridianfigur
Kulmination - obere und untere, Mittagsbreite, Zenitdistanz, Deklination, … Begriffe, die so oder so im Zusammenhang stehen mit der Berechnung der Gestirnshöhe.
Zur Veranschaulichung dieser Zusammenhänge zwischen den beteiligten Winkeln zeichnet man eine Meridianfigur. Sie hilft den Überblick zu bewahren und zum richtigen Ergebnis zu kommen, denn es gibt pro Erdhalbkugel drei verschiedene und doch typische Konstellationen:
Deklination des Gestirns und Breite des Beobachters sind gleichnamig – wobei entweder die Deklination oder die Breite ist größer sein kann – oder beide sind ungleichnamig. Und oft muss man wieder darüber nachdenken, wie nun nochmal die Zusammenhänge und schließlich die Rechenwege sind.
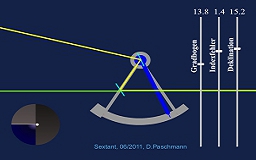
Nun, der Beobachter misst die Höhe eines Gestirns mit dem Sextanten mit Bezug auf seinen Horizont. Der Gegenwinkel zu dieser Höhe ist die sogenannte Zenitdistanz. Beide zusammen gezählt ergeben 90°. Die Deklination des beobachteten Gestirns jedoch bezieht sich auf den Himmelsäquator. Und schließlich ergibt die Deklination zusammen mit der Zenitdistanz und noch dem Gegenwinkel der Beobachtungsbreite zusammen einen zweiten rechten Winkel.
Da Zenitdistanz und die Breite des Beobachters an beiden 90°-Winkeln beteiligt sind, kann man deshalb die fehlenden Beträge ermitteln.
Man stelle die Deklination des Gestirns ein und die Beobachtungsbreite. Daraus gehen die einzelnen Winkel und ihre Lage in der Darstellung hervor. Die Höhe kann man anschließend nachmessen bzw. grob bestätigen.
Einige Bezeichnungen wurden hier bewusst nicht so präzise wiedergegeben, wie es ginge. So gibt es beispielsweise einen klaren Unterschied zwischen der beobachteten und der berechneten Höhe des Gestirns über dem wahren Horizont des Beobachters. Unter dieser Präzisierung würde die Darstellung leiden. Sie ist Teil eines anderen Rechenschritts.
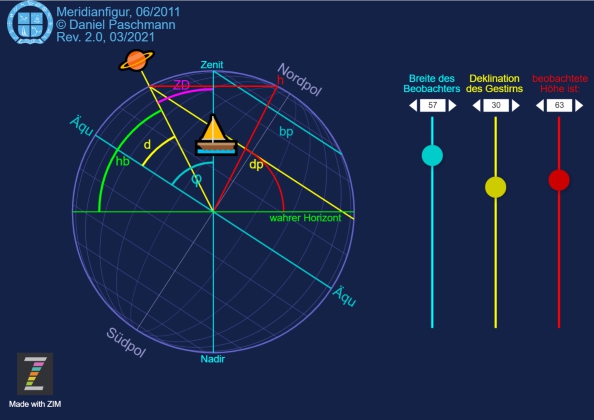
Die Höhensituation von der Seite
Durch diesen Schnitt werde die Zusammenhänge zwischen Breite, Deklination, Gestirnshöhe, Horizont und Zenit sichtbar
Animation - Astronavigation
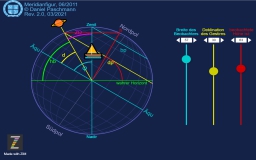
Polfigur
In der Polfigur wird die Beziehung der unterschiedlichen Stundenwinkel in Zusammenhang gebracht.
Mit der Sicht aus der Vogelperspektive auf den Pol beginnt es bei dem Meridian von Greenwich und endet beim Ortsstundenwinkel des Gestirns. Dazwischen die Länge des Beobachters und gegebenenfalls der Frühlingspunkt. Mit einer Zeichnung der Zusammenhänge bzw. dieser Animation verschafft man sich schnell den Überblick.
Wie groß ist der Ortsstundenwinkel t zwischen Beobachter und dem beobachteten Gestirn – sei es Sonne, Planet oder Stern? Sein Wert geht in die Berechnung der gerechneten Höhe und natürlich des Azimuts ein.
Im Falle von Sonne und Planeten werden Ortsstundenwinkel des Beobachters und der Greenwicher Stundenwinkel des Gestirns zusammengezählt – der eine vollkreisig von 0° – 360°, der andere halbkreisig von -180° - +180°. Oder anders gesagt: ein westlicher Ortsstundenwinkel des Beobachters wird vom Stundenwinkel des Gestirns abgezogen – ein östlicher hinzuaddiert.
Im Falle von Sternen findet man im Jahrbuch statt dessen den Greenwicher Stundenwinkel des Frühlingspunktes, zu welchem der Sternenwinkel beta bzw. siderische Stundenwinkel des Gestirns hinzuaddiert wird.
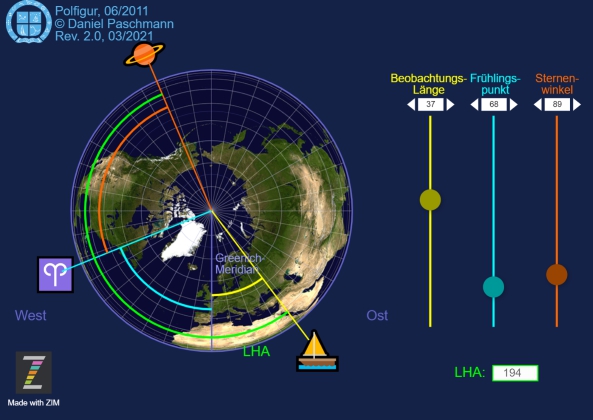
Zusammenhang zwischen Grt, t, lambda und beta für einen Beobachter.
Einen schnellen Überblick verschaffen über die Größe des Stundenwinkels des beobachteten Gestirns am Ort der Beobachtung – das ermöglicht diese kleine „App“.
Animation - Astronavigation
Grosskreis
Die kürzeste Entfernung zwischen zwei beliebigen Orten auf der Erde liegt genau auf einer Verbindungslinie, die Teilstrecke eines Großkreises ist. Um zu verstehen, wie sich aus zwei Orten auf der Erdoberfläche der zugehörige Großkreis entwickelt und legt, soll diese Animation eine Hilfe sein. Breite und Länge eines Abfahrtsortes A und Zielortes B können gewählt werden, womit sich der dazu passende Großkreis einstellt. Würde man von A nach B segeln wollen, könnte man auch noch den Abfahrts- und Zielkurs grob erkennen.
Ein Großkreis ist ein Kreis um die Erde, dessen Mittelpunkt der Erdmittelpunkt ist. Die kürzeste Verbindung zwischen zwei beliebigen Punkten auf der Erdoberfläche (--> Kugel) findet man, wenn man den Großkreis sucht, auf dem die beiden Punkte liegen.
Man stelle Breite und Länge der beiden Punkte A und B ein und die Animation berechnet dazu den passenden Großkreis.
Mathematisch geht es etwa so: Auf die Fläche, die sich zwischen den beiden Vektoren zwischen Erdmittelpunkt und den Punkten A und B aufspannt, steht ihr Normalenvektor senkrecht. Dieser definiert den zu diesen beiden Punkten gehörenden Großkreis, denn der liegt senkrecht zu diesem Vektor. Der Großkreismittelpunkt – selbstredend – liegt ebenfalls im Erdmittelpunkt.
Dunkelblau ist der Greenwich-Meridian. Das Startbeispiel zeigt die kürzeste Verbindung zwischen Boston und dem Eingang des Englischen Kanals, auf den man leicht von Norden kommend einbiegt, obwohl Boston einige 8° weiter Südlich liegt.
Zur besseren Betrachtung lässt sich die Erde neigen und um ihre Achse rotieren.
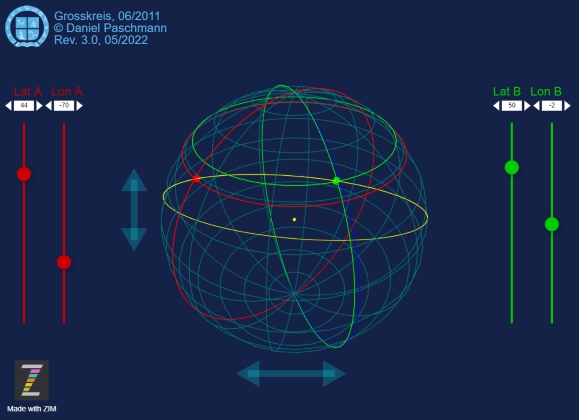
Kürzeste Verbindungslinie zwischen zwei Orten auf dem Großkreis
Ein Großkreis ist ein Kreis auf der Erdoberfläche um die Erde herum und mit dem Erdmittelpunkt als Mittelpunkt.
Animation - Astronavigation
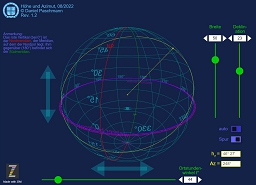
Höhe und Azimut
Abbildung der Formeln des spärischen astronomischen Dreiecks.
Und auch hier wieder: Einstellen - ablesen - fertig!
Bekanntlich werden aus der Breite des Beobachters, der Deklination des beobachteten Gestirns und dem Stundenwinkel zwischen Beobachter und Gestirn die gerechnete Höhe und das Azimut berechnet. Das macht diese Animation und noch einiges mehr:
Spielerische Gewinnung eines Verständnisses für die Sternenbewegung am Nacht- und TagHimmel
Überschlägige Bestimmung von hr und Az im Vorfeld einer Messung
Sichtbarmachung des Pfades eines Gestirns während der Drehung der Erde
Untersuchung Nordstern, seiner Lage und Bewegung
Untersuchung Sonne: Tag-/Nachtgleichen, Sonnenwenden, Polarkreise, …
u.v.a.m.
In dieser App lassen sich die Breite und die Deklination eines Gestirns wählen. Im „auto“-Modus wird die Gestirnsbahn abgefahren und per „Spur“ auch gezeichnet. Der laufende Parameter hierbei ist der Stundenwinkel. Ist „auto“ inaktiv kann ein beliebiger oder spezieller Stundenwinkel manuell gewählt werden. Bei jeder Veränderung werden die gerechnete Höhe und das Azimut nach den einschlägigen Formeln bestimmt.
Die Maßstäbe an der Himmelskugel sind die Höhe über dem wahren Horizont und das Azimut.
Zur besseren Betrachtung einer Situation kann die Weltkugel mit Hilfe der türkisen Pfeile um die Achse „Zenit-Nadir“ rotiert werden, die Weltkugel lässt sich zum Zenit oder Nadir neigen.
Außerdem kann in die Erdkugel hineingezoomt werden und zurück mit dem zunächst kaum sichtbaren Pfeil unterhalb des „Weltmittelpunktes“. Maus gedrückt halten beim Schieben über die Pfeile.
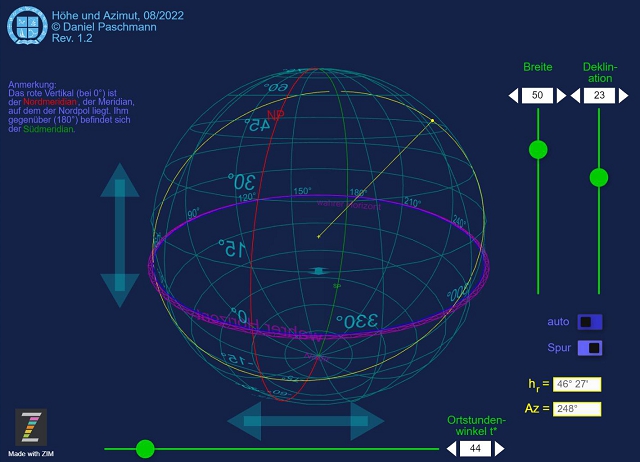
Umsetzung der Formeln für das Sphärisch-astronomische Dreieck.
Ergebnisse leicht zu erzielen: Breite und Deklination einstellen, Stundenwinkel wählen und schon werden gerechnete Höhe und Azimut berechnet und angezeigt. Selbst die Bahn des Gestirns um den Beobachter!
Animation - Astronavigation
Höhenstandlinien
Ein Zeichen-Tool für die Positionsbestimmung nach der Berechnung der Gestirnshöhen.
Mit den errechneten Azimuten und Intercepten für verschiedene Gestirne wird die Position zeichnerisch bestimmt. Für 2 oder 3 Gestirne berechnet dieses Tool den beobachteten Ort aus den vorher berechneten Daten.
Einstellen - ablesen - fertig!
Der Vorgang war wie folgt: Mit dem Sextanten die beobachteten Gestirnshöhen messen, mit Hilfe des Nautischen Jahrbuches, der Sight Reduction Tables und des Nautical Almanac daraus die rechnerischen Höhen und Azimute berechnen. Anschließend wird das jeweilige Intercept durch Vergleich gewonnen. Sind dann alle berechneten Werte verglichen und überprüft, werden die Daten ins Astro-Plottingsheet übernommen, die Standlinien entsprechend eingezeichnet und am Ende der beobachtete Ort zeichnerisch bestimmt.
Die Standliniendaten für bis zu drei Gestirne können hier eingegeben werden, woraus der Ob berechnet wird in Distanz und Richtung bzw. Abweitung und Breitenunterschied.
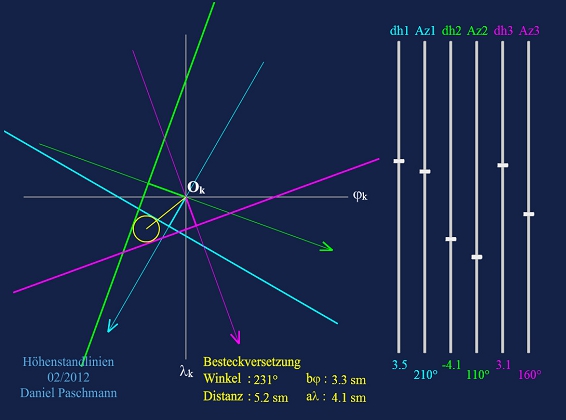
Bestimmung des beobachteten Ortes mit Höhenstandlinien
Diese kleinen „App“ nimmt die berechneten Standliniendaten und bestimmt daraus "zeichnerisch" den Schnittpunkt bzw. den Mittelpunkt des Positionsdreiecks.
Animation - Funk
Frequenzmischer
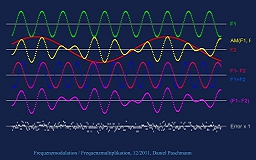
Das ist eigentlich phänomenal für den Normalbürger – Handwerkszeug jedoch für den Elektrotechniker: Das Signal, dass sich aus der Modulation einer Frequenz (grün) mit einer zweiten (rot) ergibt (gelb), ist quasi gleich mit dem Signal, das sich aus der Multiplikation (violett) der Differenz beider Frequenzen (dunkelrot) mit der Summe beider Frequenzen (blau) berechnet.
Hier werden nur die einzelnen Signale gezeigt.
Und ja: Das multiplizierte Signal ist eigentlich doppelt so groß, und irgendwo gibt es noch eine Phasendrehung … Aber cool ist, dass die Kurvenformen so übereinstimmen.
Was man damit anfängt? Nichts! Kommt das in der LRC-Prüfung dran? Nein!
Hat nur didaktischen Wert für Interessierte.
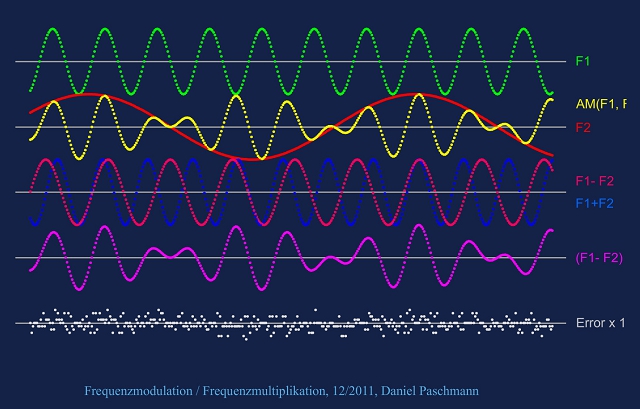
Komplexe Mathematik der Elektrotechnik
Was ist Modulation? Eine komplexe Berechnung von zwei Signalen über Summe, Differenz und Produkt. Ganz einfach!
Animation - Astronavigation - Komponenten
Sextant
Beschreibung kommt in Kürze ...
Derzeit leider nicht verfügbar (Flash!).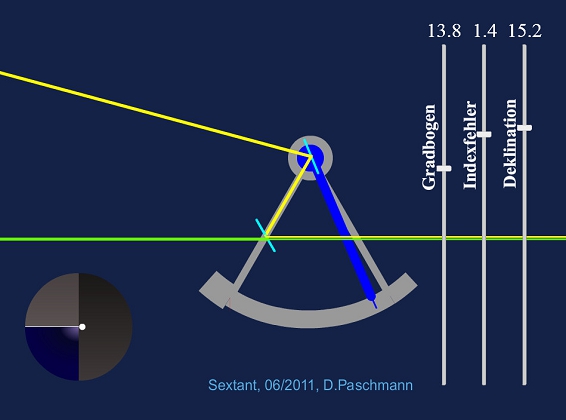
Animation - Astronavigation
Schalttafel
Eine Erleichterung für den zeitgestressten Anwender der Schalttafel am Ende des Nautischen Jahrbuches.
Einstellen - ablesen - fertig!
Die berechneten Werte sind mit denen des Nautischen Jahrbuches identisch.
Das Aufsuchen des Wertes Verbesserung (Vb) in der Schalttafel aus den Eingangsgrößen Stunde, Minute und Unterschied (Unt) nimmt mitunter einige Zeit in Anspruch. Ebenfalls besteht erfahrungsgemäß in der Eile die Gefahr, den Wert aus der falschen Seite des Nautischen Jahrbuchs auszulesen. Etwas schneller und einfacher geht es mit dieser kleinen App: Stunde und Minute geschwind einstellen und den Verbesserungswert für den gegebenen Unterschied ablesen. Zudem wird für den Zeitunterschied der Zuwachs Grt für Sonne, Frühlingspunkt und Mond berechnet.
Derzeit leider nicht verfügbar (Flash!).
Berechnung der Schalttafelwerte
Mit Hilfe dieser kleinen „App“ geht die Berechnung schneller und manchmal kann ein Ablesefehler vermieden werden.
Animation - Radar - Komponenten
Radar-Einstellung
Wie hängen die für das Erkennen von Objekten wichtigsten Einstellgrößen eines Radargerätes zusammen?
Das zu erklären ist der Inhalt diese Radar-Simulation.
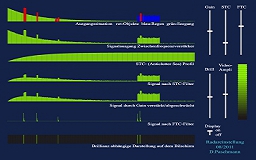
Mit den Einstell-Funktionen des Bildschirms Brilliance und Kontrast sowie den Reglern Gain, STC und FTC, die in die Signalverstärker-Elektronik eingreifen, muss gezielt gearbeitet werden (können), um nicht einerseits einen schwarzen Bildschirm zu betrachten, ebenso wenig wie andererseits einen hell-leuchtend gefluteten Bildschirm.
Zuerst verwendet man den Einstellregler Brilliance. Er wirkt auf die Bildschirm-Gesamthelligkeit. Nicht zu hell und auch nicht zu dunkel, damit die Anzeige weder überstrahlt ist noch gar nichts zu sehen ist. Der Bereich zwischen hell und dunklen Stellen soll nicht fließend sein sondern hell oder dunkel. Dies regelt Kontrast, der auf den Videoverstärker arbeitet. Der Farbbalken rechts soll eigentlich den ganzen Farbbereich gut von ganz hell bis ganz dunkel abbilden.
Gain verändert sich mit dem Entfernungsbereich, wobei in höheren die Impulsdauer (Paketlänge) vergrößert wird – also mit mehr Energie gesendet wird. Also muss ständig entsprechend das Gain angepasst werden.
Mit FTC (Fast Time Constant = Regenenttrübung) sowie STC (Sensitivity Time Control = Seegangsenttrübung) kann die Abbildung noch einmal wesentlich verbessert werden.
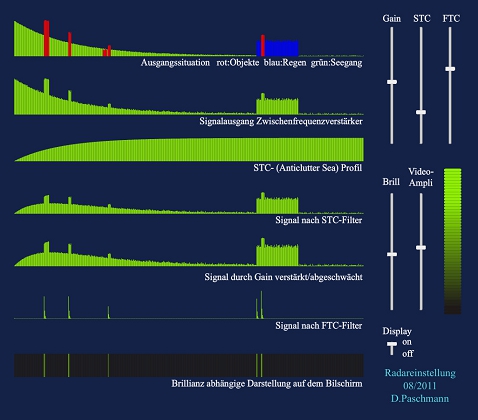
Nachbildung der Radar-Einstellregler
Lernen, in welcher Reigenfolge die Einstellungen am Radargerät vorgenommen werden müssen und wie sie sich auf den und auf dem Bildschirm auswirken.
Animation - Radar - Navigation - KVR
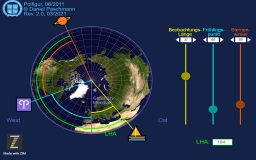
Radartrainer
Die Simulation eines Radargerätes, wie es dann zur Navigation eingesetzt wird und zur Beurteilung, ob die Möglichkeit der Gefahr einer Kollision besteht, so wie es in den KVR verlangt wird.
Alle typischen Einstellfunktionen wie Range, Spur und Spurlänge (in Minuten), EBL und VRM, Display-Modes sind vorhanden. Darüber hinaus für die eigene Schiffssteuerung Geschwindigkeit und Kurs und – da wir ja nicht ewig Zeit haben – einen Beschleunigungsfaktor im Vergleich zur Echtzeit (Time Scale).
Man stelle sich das Radargerät ordentlich ein und stelle sich dabei einen der gängigen Display-Modes (Head-Up, North-Up oder Course-Up) ein. Kurs und Geschwindigkeit stehen bereits an, können auch verändert werden, jedoch startet die Simulation pausiert. Sobald die Simulation läuft bilden sich die Echo-Trails aus, Standard-Einstellung sind 10 Minuten.
Das Verändern des Zeitmaßstabes (Time Scale) – das gibt es nur an diesem Radargerät – lässt die Zeit entsprechend schneller vergehen.
Es lassen sich nun die Bewegungen der Ziele analysieren, deren absolute Kurse und absolute Geschwindigkeiten berechnen – insbesondere unter Einsatz von EBL und VRM, sobald ein Echo-Trail die nominale Länge erreicht hat. Achtung: im wahren Leben werden die Trails gelöscht, sobald man den Entfernungsbereich wechselt.
Bald gibt es auch ein paar Aufgaben-Files.
Ein Page-Reload (F5) startet mit neuen Daten (Objekten).
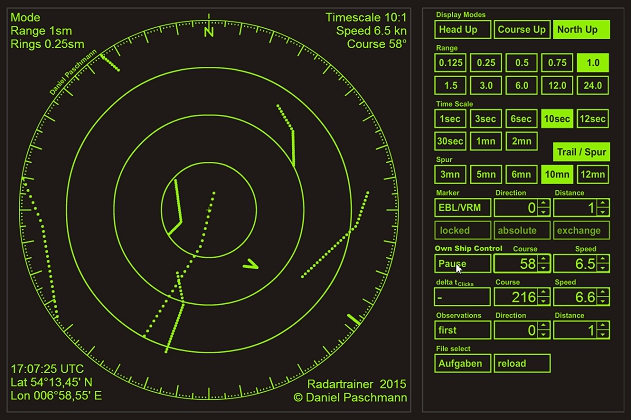
Radar, wie es zur Navigation eingesetzt wird
Die vollständige, nicht elektronische Simulation eines Radargerätes mit allen gängigen Einstellmöglichkeiten.
Alle Inhalte dieser Website sind urheberrechtlich geschützt. Jegliche Nutzung von Inhalten, Texten, Grafiken und Bildern dieser Website ist ohne ausdrückliche schriftliche Zustimmung der Yachtsegelschule Karlsruhe unzulässig. Dies gilt insbesondere für die Verbreitung, Vervielfältigung und öffentliche Wiedergabe sowie Speicherung, Bearbeitung oder Veränderung. Alle Rechte bleiben vorbehalten.
©
2018 - 2024
Yachtsegelschule Karlsruhe